Random Variables in Statistics

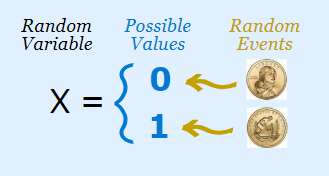
A Random Variable is any rule that maps (links) a number with each outcome in sample space S.

Mathematically, random variable is a function with Sample Space as the domain. It’s range is the set of Real Numbers.

Random Variables are represented by English Uppercase letters. Their instances are represented by English Lowercase letters.

Ex : X = x means X is the Random Variable and x is an instance of X.

Example 1

When a person calls a customer care hotline of a bank, an operator might pick up immediately (Success – S) or that person might be put on hold by the operator for a while (Failure – F).

Sample Space = {S,F}

Random Variable X can be defined as, X(S) =1 and X(F)=0. This means if the operator picks up immediately, value of X is 1 and if the operator puts the person on hold, the value of X=0.

Bernoulli Random Variables

When a random variable has only two possible values 0 & 1 is called a Bernoulli Random Variable.

Example 2

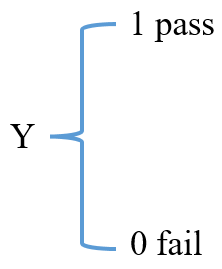
In a particular exam, students are considered as Pass if the score is over 75% & fail if otherwise. For this scenario, we can define a Random Variable as follows;

In some experiments, we can define several random variables.

Example 3

Consider an experiment where a coin is tossed until a head turns upwards.

Sample Space = {S,FS,FFS,…}

X = no of times coins is tossed before a head turn upwards.

X(S) = 1, X(FS) = 2, X(FFS) = 3, … and so on.

In this case, it is clear that any positive integer is a possible value of X. Therefore the set of possible values is infinite.

Types of Random Variables

There are 2 types;

1. Discrete Random Variables
   • It can be listed in an infinite sequence in which there is a 1^st element 2^nd and so on (“countably infinite”).
2. Continuous Random Variables
   • A Random Variable is continuous is both of the following conditions are satisfied.
     1. The set of all possible values consists of either of all numbers in a single interval on the number line. (ex : – from -∞ to +∞) or all numbers in a disjoint union of such intervals (ex: – [0,5] U [10,15]).
     2. Any possible value of the variable does not have a positive probability. That is, P(X=C) = 0 for any possible value c.

Conclusion

Random Variables are a very essential concept in the study of Statistics and Probability. In our next tutorials, we will study probability distributions related to Discrete Random Variables.