Probability Mass Function

Introduction to PMF

Probability Mass Function, PMF of the Random Variable X says how the total probability of 1 is distributed or allocated to among the various possible X values.

Definition of Probability Mass Function

The Probability Mass Function, P(X = x), f(x) of a discrete random variable X is a function that satisfies the following properties.

This means for every element x in the sample space S, all the probabilities must be positive. That is, if x does not belong in the sample space S, then f(x) = 0

If you add up the probabilities for all of the possible x values in the Sample Space S, then the sum must equal to 1.

To determine the probability associated with event A, you must sum up the probabilities of X values in A.

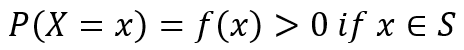
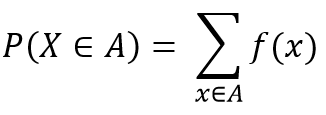
Descriptive Example

Consider a Mobile Phone manufacturing factory. Suppose they have prepared 5 boxes of Mobile Phones to be delivered to 5 different customers.

The number of defective mobile phones in each box are as follows;

One of these boxes will be selected to send to a customer.

Let X be the number of defectives in the selected box.

3 possible values of X are 0, 1 and 2.

These are 5 equally likely simple events.

Probability Mass Function of X is;

p(0) = P(X=0) = P(box 1 or 2 sent) = 2/5 = 0.4

p(1) = P(X=1) = P(box 3 or 5 sent) = 2/5 = 0.4

p(2) = P(X=2) = P(box 4 sent) = 1/5 = 0.2

Interpretation of Probability Mass Function

A probability of 0.4 is distributed to values 0 and 1. And a probability of 0.2 is distributed to value 2.

Values of X along with their probabilities define the PMF.

Graphical Representation of PMF

We can plot the values of p(x) against each value of x.

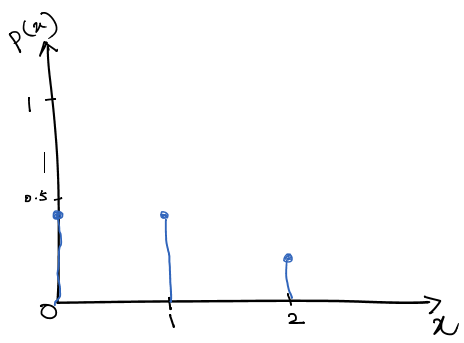
Therefore it is clear that PMF can be interpreted both Numerically and Visually.

Why it is called Probability Mass Function?

Name PMF is suggested by a model used in Physics for a system of Point Masses. In this model, masses are distributed at various locations X along a one-dimensional axis.

Our PMF describes how the total probability mass of 1 is distributed at various points along the axis of possible values of the Random Variable X (where and how much mass at each x).

Concept of Probability Mass Function will be very useful when you are studying further probability, expected values and so on.