Binomial Probability Distribution

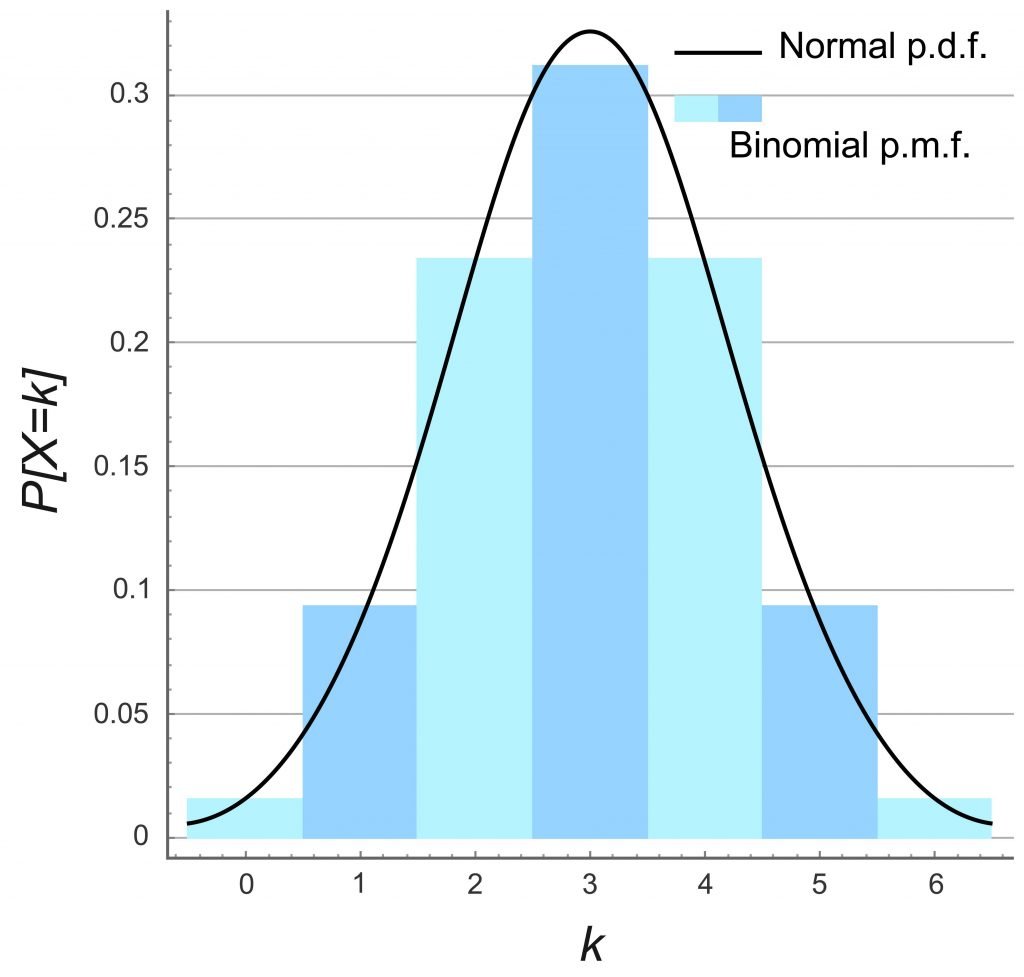
Hello guys, a good day to you! In this post, I am gonna explain everything you need to know about the Binomial Probability Distribution.

What is a Binomial Experiment?

If an experiment satisfies the following conditions, we call it as a Binomial Experiment.

The experiment consists of a sequence of n smaller experiments called trials. n is fixed before the experiment.
Each trial has only 2 outcomes. We label these two outcomes as Success (S) and Failure (F).
Trials are independent of each other.
Success(S) probability is constant from trial to trial. We represent success probability by θ.

With or Without Replacement?

In general, if we sample without replacement we will not get independent trials. Therefore this kind of experiment cannot be considered as Binomial.

But,

Assume we sample from a large population where sample size n is approximately about 5% of the population. An experiment like this can be considered as a Binomial Experiment.

Distribution of Binomial Random Variable

In Binomial Experiments, we are interested in the number of Successes.

Binomial Random Variable can be defined as,

X = number of successes in n trials

Distribution of X can be represented as;

Formula

Formula to calculate probabilities associated with Binomial Responsibilities is as follows;

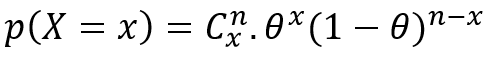
Detailed Example – 1

There is a bulb manufacturing factory. For each production batch, they manufacture 100,000 bulbs. From long term experience, the manufacturer knows that 1% of the bulbs are defective from a batch of 100,000 bulbs. A random sample of 200 bulbs is taken from a batch.

Let X be the number of defective bulbs

What is the probability that 2 bulbs are defective?
What is the probability at least 1 bulb is defective?

Answer

Distribution of our random variable is;

Here θ = 0.01.

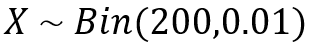
The solution to the first part is as follows;

$\begin{align*} P(X=x) &= \binom{n}{x}\theta^x(1-\theta)^{n-x}\\ P(X=2)&= \binom{200}{2}(0.01)^2(1-0.01)^{198}\\ P(X=2)&=19900*0.01^2*0.99^{198}\\ P(X=2)&=\underline{\textbf{0.272}} \end{align*}$

The solution to the second part;

$\begin{align*} P(X\leq1)&= P(X=0)+P(X=1)\\ P(X\leq1)&=\binom{200}{0}(0.01)^0(1-0.01)^{200-0} +\binom{200}{1}(0.01)^1(1-0.01)^{200-1} \\ P(X\leq1)&= 1*1*0.99^{200} + 200*0.01*0.99^{199}\\ P(X\leq1)&= 0.134+0.271\\ P(X\leq1)&=\underline{\textbf{0.405}} \end{align*}$

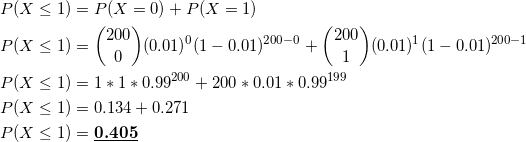
Detailed Example – 2

30% of all refrigerators require repairs during the warranty period. From this 30%, 70% can be repaired and the remaining 30% should be replaced with new refrigerators. Suppose, a person buys 15 refrigerators for charity, calculate the probability that 3 refrigerators will be replaced during the warranty period.

Answer

First let’s define our random variable as follows;

X – number of refrigerators replaced during the warranty period

We should find P(X = 3)

We know that n=15 and the success probability in our experiment = 0.3*0.3 = 0.09

Therefore θ = 0.09 .

X ~ Bin(15,0.09)

$\begin{align*} P(X=x) &= \binom{n}{x}\theta^x(1-\theta)^{n-x}\\ P(X=2) &= \binom{15}{3}\0.09^2(1-0.09)^{15-3}\\ P(X=2)&=\underline{\textbf{0.107}} \end{align*}$

Mean and Variance of X

When n=1, binomial distribution behaves like a Bernoulli Distribution. The mean value of Bernoulli Distribution is θ. So the expected number of success in any single trial is θ.

A Binomial Experiment consists of n trials. Therefore it’s intuitive that for X~Bin(n,θ) is $E(X) = nθ

V(X) = nθ(1-θ) and σ_x = √nθ(1-θ)

What is a Binomial Experiment?

With or Without Replacement?

Distribution of Binomial Random Variable