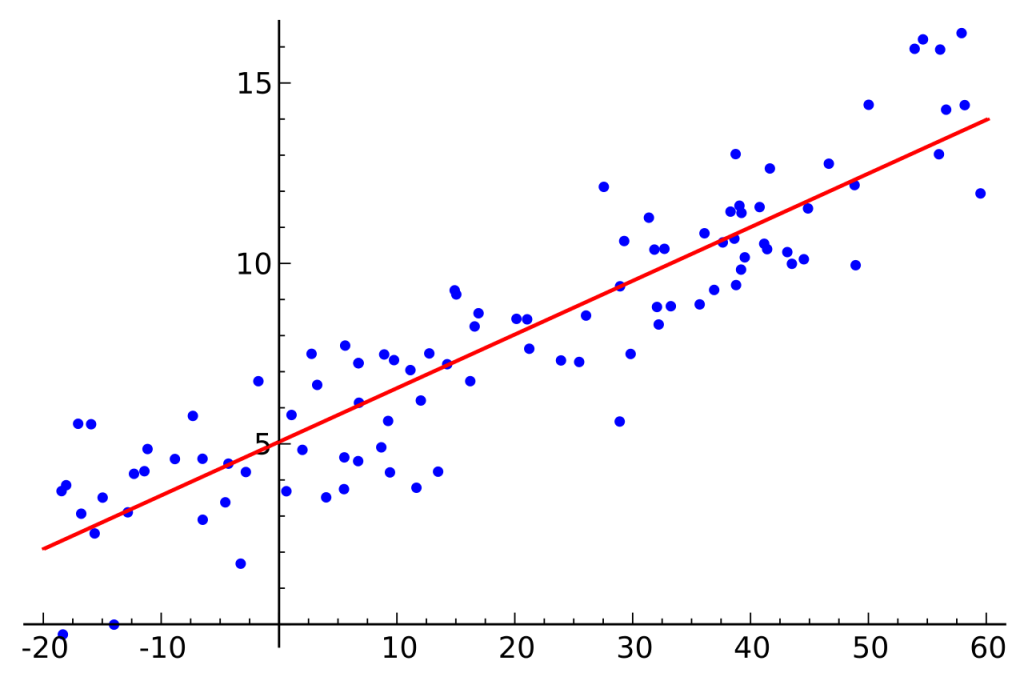
When studying statistics, many times you have come across the term “Expected Value”. We came across it in the post on Simple Linear Regression also. Ever wondered what it means? In this post, we are gonna explain to you the concept behind Expected Value.
What is the meaning of Expected Value?
Expected Value is the average value we get for a certain Random Variable when we repeat an experiment a large number of times. In other words, it can be defined as the ‘theoretical mean’ of a random variable.
It is not based on sample data. It is based on the population. Therefore it is a parameter, not a statistic.
Expected Value can be calculated from the following formula;

Detailed Example – 1
Suppose a dice is rolled a large number of times. We are interested in which side is turned upwards.
Here any side turning upwards is equally likely to occur. Since expected value is equal to the mean of the distribution, it can be calculated simply as the average of 1,2,3,4,5,6. The answer is 21/6 = 3.5. Let’s see how we can calculate that using probabilities;
In this case, our Random Variable can be defined as;
X = side turned upwards
In this table, you can find Probabilities for each possible value of X and the values for x.P$(x)$. This “x.$P(x)$” term is referred to as “Probability Mass Function” in Statistics. It is denoted by ‘$p(x)$’. You can find more details about the Probability Mass function by clicking here.
| x | Probability $P(x)$ | x.$P(x)$ |
| 1 | 1/6 | 1/6 |
| 2 | 1/6 | 2/6 |
| 3 | 1/6 | 3/6 |
| 4 | 1/6 | 4/6 |
| 5 | 1/6 | 5/6 |
| 6 | 1/6 | 6/6 |
$E(x)$ for this scenario can be calculated as below;
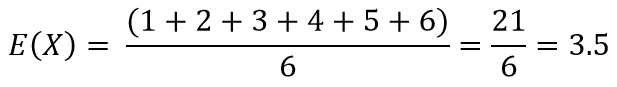
Okay, now we have got the Expected value of this experiment as 3.5. This means, when you roll this unbiased dice infinite no. of times, on average 3.5 side will turn upwards. Seems unrealistic but in this case that’s what it means.
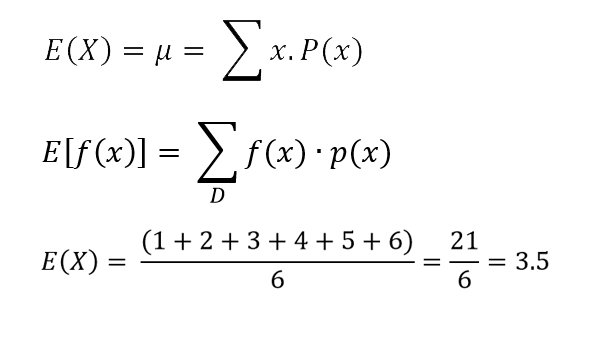
The Expected Value of a Function
Sometimes, we have to find the Expected Value of Functions too.
Suppose $f(x)$ is a function. Random Variable X has a set of possible values D and $p(x)$ is the Probability Mass Function. Then the $E(x)$ of $f(x)$ can be calculated from the formula below;

Rules of Expected Value
If the function $f(x)$ is of the linear form aX+b. And ‘a’ and ‘b’ are constants, $E[f(x)]$ can be calculated as below;

There are another 2 important rules;
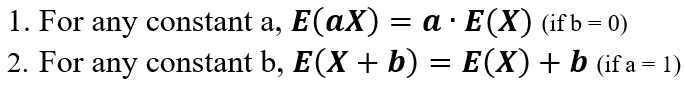
Okay, we have learned a considerable amount of fundamentals about Expected Values. I hope you all now have the idea of it. We will discuss this more with detailed examples in a future post.