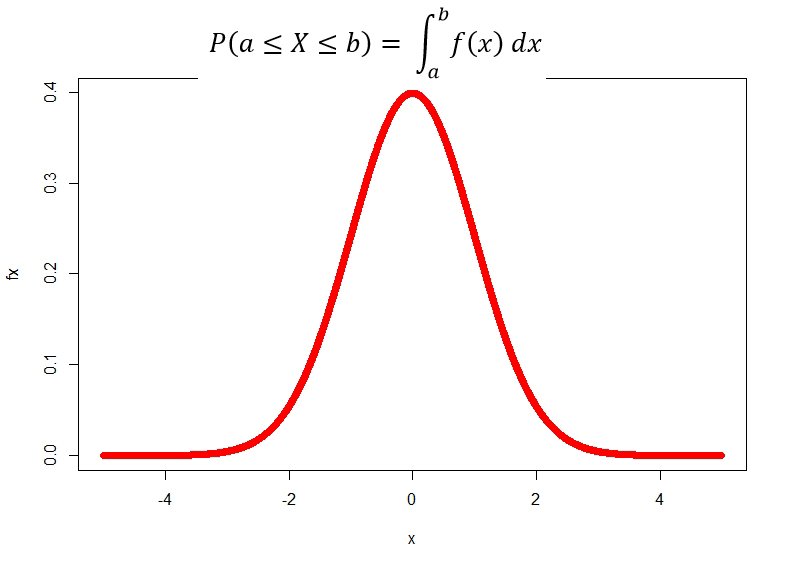
Earlier we used Probability Mass Function to describe how the total probability of 1 is distributed among the possible values of the Discrete Random Variable X. But we cannot define Probability Mass Function for a Continous Random Variable. We use the Probability Density Function to show the distribution of probabilities for a continuous random variable.
Definition
Let X be a continuous random variable. Then a probability distribution function (pdf) of X is a function f(x); such that for any two numbers a and with a ≤ b;
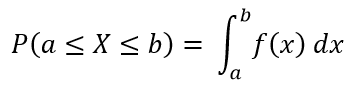
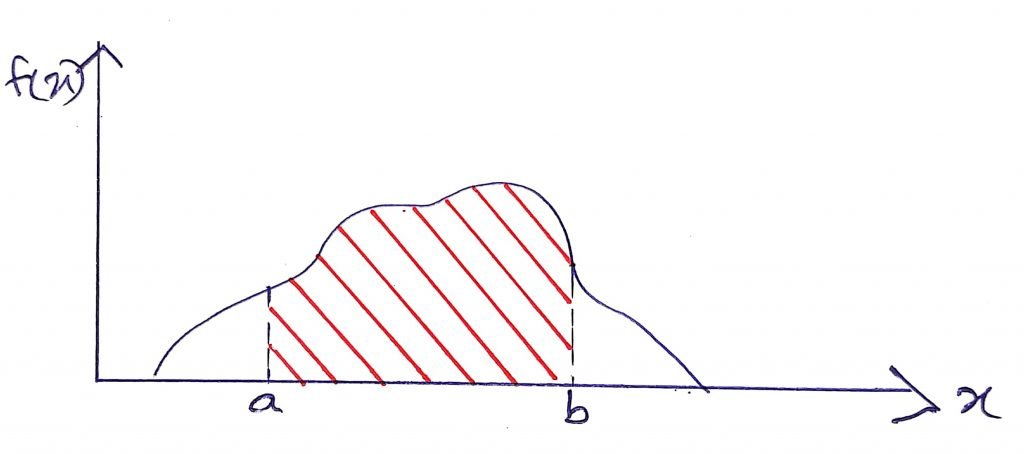
f(x) should satisfy the following 2 conditions:
- f(x) > 0 for all x
- Integral
is equal to the area under the graph of f(x) which is equal to 1
Detailed Example
Let X be a continous random variable whose probability density function is;
f(x) = 2x2 for 0< x <1
But f(x) ≠ P(X = x)
ex : f(2) = 2(2)2 = 4 this is clearly not a probability.
f(x) is the height of the curve at X = x so that the area under the curve is 1.
In our future posts, we will be discussing about several probability density functions such as Uniform Distribution, Normal Distribution, Gamma Distribution etc.
