Introduction for Poisson Distribution
A discrete random variable follows a Poisson Distribution with parameter λ (λ >0) if the probability mass function of X is;
(1) 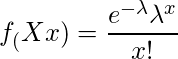
Here, the term ![]() is the Expected Value of the Random Variable X. Expected Value can also be defined as the mean of a Random Variable. If want to know more about what expected value is, please refer this post.
is the Expected Value of the Random Variable X. Expected Value can also be defined as the mean of a Random Variable. If want to know more about what expected value is, please refer this post.
It is named after the French Mathematician Simeon Denis Poisson.
Poisson Distribution outputs the probability of a sequence of events happening in a fixed time interval.
Detailed Example for Poisson Distribution
Ministry of Transportation has conducted a research for a period of 12 months and have found that 15 road accidents occur in a small city City monthly. Let random variable X be the number of accidents happening per month. Assume X follows a poisson distribution. Calculate the probability that 18 accidents happening in a particular month.
Here we have to find ![]() .
.
According to the given data, parameter ![]()
Now we just have to plug in the figures to our equation;

Poisson Approximation to Binomial Distribution
Consider a Binomial Experiment where we have a large sample of size n and a fairly small success probability ![]() .
.
Then;
Bin(n,θ) ≈ Poisson(λ)
Formal Definition of the approximation
Consider probability mass function of Binomial Distribution Bin (n,θ). When n → ∞ and θ → 0 in such a way that nθ approaches a value λ>0.
Then Bin(n,θ) ≈ Poisson(λ)
In general, for the above to be true, n>50 and nθ <5 .
Example for Poisson Approximation
[The following example was extracted from the book Probability and Statistics for Engineering and the Sciences by jay l devore]
A book publisher notices that the probability of any given page containing at least one typographical error is 0.005, and errors are independent from page to page. What is the probability that one of the 400 page books will contain exactly one page with errors?
First, let’s use Binomial Distribution to calculate the probability.
Let X be a Binomial Random Variable with n=400 and θ = 0.005

Now let’s calculate the Probability using Poisson Distribution
Let Y be a Poisson Random Variable. Expected value of Y is ![]() . Therefore
. Therefore ![]() .
.
When we substitute values into our poisson equation;

Therefore it is clear that in this problem, probability can be calculated by using both methods and we get the exact same answer.
In the above example ![]() which is <5 and n=400 which is >50. Hence, we can calculate probabilities using the poisson distribution in situations like these.
which is <5 and n=400 which is >50. Hence, we can calculate probabilities using the poisson distribution in situations like these.
Poisson Process
Occurence of events over a time is called a Poisson Process. We introduce a parameter called ![]() which specify the rate for the process.
which specify the rate for the process.
Assumptions about the Poisson Process
- There exists a parameter
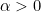 such that for any short time interval of length
such that for any short time interval of length 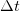 , probability that exactly one event occurs is
, probability that exactly one event occurs is 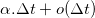
- In other words, the above assumption states that for a short interval of time, the probability of a single event occurring is approximately proportional to the length of the time interval, where
 is the constant of proportionality.
is the constant of proportionality.
- In other words, the above assumption states that for a short interval of time, the probability of a single event occurring is approximately proportional to the length of the time interval, where
- The probability of more than one event occurring during
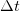 is
is  . Therefore, when considering with first assumption, it can be implied that the probability of no events during
. Therefore, when considering with first assumption, it can be implied that the probability of no events during 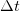 is
is 
- No. of events occurring during the time interval of
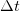 is independent of the number that occur prior to this time interval.
is independent of the number that occur prior to this time interval.
probability that k events will be observed during any particular time interval of length t
(2)
so that the number of events during a time interval of length t is a poisson random variable with parameter ![]()
Expected number of events during any such time interval is then ![]() , so the expected number during a unit interval of time is
, so the expected number during a unit interval of time is ![]() .
.

